Using the Fixed Variance process¶
The FixedVariance volatility process can be used to implement zig-zag model estimation where two steps are repeated until convergence. This can be used to estimate models which may not be easy to estimate as a single process due to numerical issues or a high-dimensional parameter space.
This setup code is required to run in an IPython notebook
[1]:
import matplotlib.pyplot as plt
import seaborn
seaborn.set_style("darkgrid")
plt.rc("figure", figsize=(16, 6))
plt.rc("savefig", dpi=90)
plt.rc("font", family="sans-serif")
plt.rc("font", size=14)
Setup¶
Imports used in this example.
[2]:
import numpy as np
Data¶
The VIX index will be used to illustrate the use of the FixedVariance process. The data is from FRED and is provided by the arch package.
[3]:
import arch.data.vix
vix_data = arch.data.vix.load()
vix = vix_data.vix.dropna()
vix.name = "VIX Index"
ax = vix.plot(title="VIX Index")
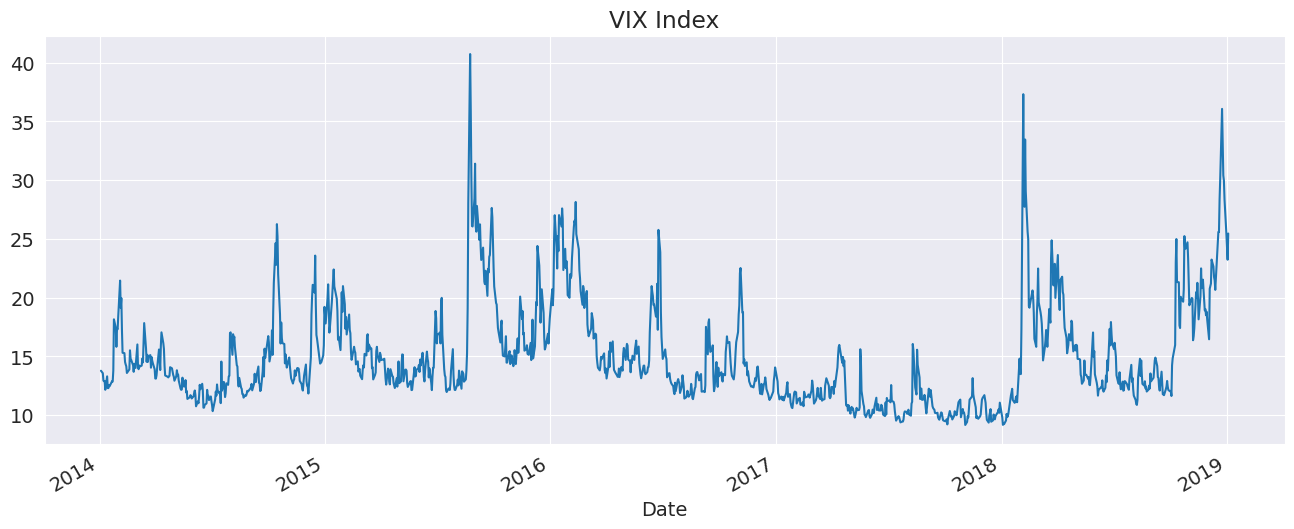
Initial Mean Model Estimation¶
The first step is to estimate the mean to filter the residuals using a constant variance.
[4]:
from arch.univariate.mean import HARX, ZeroMean
from arch.univariate.volatility import GARCH, FixedVariance
mod = HARX(vix, lags=[1, 5, 22])
res = mod.fit()
print(res.summary())
HAR - Constant Variance Model Results
==============================================================================
Dep. Variable: VIX Index R-squared: 0.876
Mean Model: HAR Adj. R-squared: 0.876
Vol Model: Constant Variance Log-Likelihood: -2267.95
Distribution: Normal AIC: 4545.90
Method: Maximum Likelihood BIC: 4571.50
No. Observations: 1237
Date: Tue, Nov 05 2024 Df Residuals: 1233
Time: 17:50:47 Df Model: 4
Mean Model
================================================================================
coef std err t P>|t| 95.0% Conf. Int.
--------------------------------------------------------------------------------
Const 0.6335 0.189 3.359 7.831e-04 [ 0.264, 1.003]
VIX Index[0:1] 0.9287 6.589e-02 14.095 4.056e-45 [ 0.800, 1.058]
VIX Index[0:5] -0.0318 6.449e-02 -0.492 0.622 [ -0.158,9.463e-02]
VIX Index[0:22] 0.0612 3.180e-02 1.926 5.409e-02 [-1.076e-03, 0.124]
Volatility Model
========================================================================
coef std err t P>|t| 95.0% Conf. Int.
------------------------------------------------------------------------
sigma2 2.2910 0.396 5.782 7.361e-09 [ 1.514, 3.068]
========================================================================
Covariance estimator: White's Heteroskedasticity Consistent Estimator
Initial Volatility Model Estimation¶
Using the previously estimated residuals, a volatility model can be estimated using a ZeroMean. In this example, a GJR-GARCH process is used for the variance.
[5]:
vol_mod = ZeroMean(res.resid.dropna(), volatility=GARCH(p=1, o=1, q=1))
vol_res = vol_mod.fit(disp="off")
print(vol_res.summary())
Zero Mean - GJR-GARCH Model Results
==============================================================================
Dep. Variable: resid R-squared: 0.000
Mean Model: Zero Mean Adj. R-squared: 0.001
Vol Model: GJR-GARCH Log-Likelihood: -1936.93
Distribution: Normal AIC: 3881.86
Method: Maximum Likelihood BIC: 3902.35
No. Observations: 1237
Date: Tue, Nov 05 2024 Df Residuals: 1237
Time: 17:50:47 Df Model: 0
Volatility Model
===========================================================================
coef std err t P>|t| 95.0% Conf. Int.
---------------------------------------------------------------------------
omega 0.2355 9.134e-02 2.578 9.932e-03 [5.647e-02, 0.415]
alpha[1] 0.7217 0.374 1.931 5.353e-02 [-1.098e-02, 1.454]
gamma[1] -0.7217 0.252 -2.859 4.255e-03 [ -1.217, -0.227]
beta[1] 0.5789 0.184 3.140 1.692e-03 [ 0.218, 0.940]
===========================================================================
Covariance estimator: robust
[6]:
ax = vol_res.plot("D")
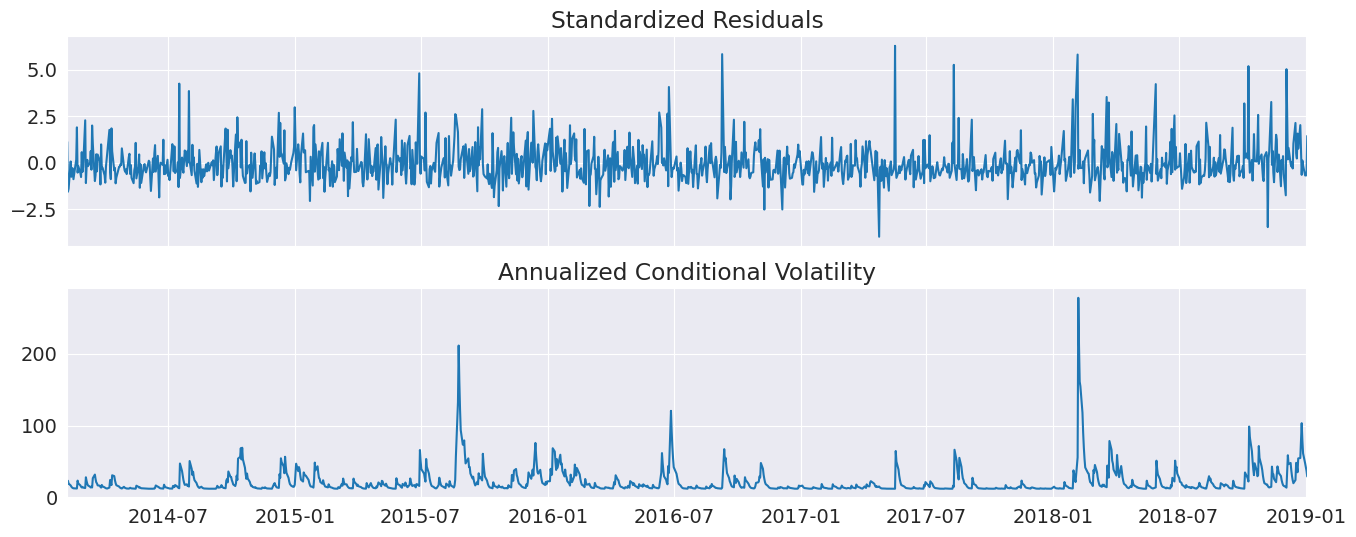
Re-estimating the mean with a FixedVariance¶
The FixedVariance requires that the variance is provided when initializing the object. The variance provided should have the same shape as the original data. Since the variance estimated from the GJR-GARCH model is missing the first 22 observations due to the HAR lags, we simply fill these with 1. These values will not be used to estimate the model, and so the value is not important.
The summary shows that there is a single parameter, scale, which is close to 1. The mean parameters have changed which reflects the GLS-like weighting that this re-estimation imposes.
[7]:
variance = np.empty_like(vix)
variance.fill(1.0)
variance[22:] = vol_res.conditional_volatility**2.0
fv = FixedVariance(variance)
mod = HARX(vix, lags=[1, 5, 22], volatility=fv)
res = mod.fit()
print(res.summary())
Iteration: 1, Func. Count: 7, Neg. LLF: 255806977215.44
Iteration: 2, Func. Count: 19, Neg. LLF: 930291.4462204215
Iteration: 3, Func. Count: 28, Neg. LLF: 3486.7135083370713
Iteration: 4, Func. Count: 36, Neg. LLF: 2885.692473212838
Iteration: 5, Func. Count: 44, Neg. LLF: 65536430.69379793
Iteration: 6, Func. Count: 53, Neg. LLF: 1935.9527543235638
Iteration: 7, Func. Count: 59, Neg. LLF: 1935.9470521680555
Iteration: 8, Func. Count: 65, Neg. LLF: 1935.9470515573437
Optimization terminated successfully (Exit mode 0)
Current function value: 1935.9470515573437
Iterations: 8
Function evaluations: 65
Gradient evaluations: 8
HAR - Fixed Variance Model Results
==============================================================================
Dep. Variable: VIX Index R-squared: 0.876
Mean Model: HAR Adj. R-squared: 0.876
Vol Model: Fixed Variance Log-Likelihood: -1935.95
Distribution: Normal AIC: 3881.89
Method: Maximum Likelihood BIC: 3907.50
No. Observations: 1237
Date: Tue, Nov 05 2024 Df Residuals: 1233
Time: 17:50:48 Df Model: 4
Mean Model
==================================================================================
coef std err t P>|t| 95.0% Conf. Int.
----------------------------------------------------------------------------------
Const 0.5584 0.153 3.661 2.507e-04 [ 0.260, 0.857]
VIX Index[0:1] 0.9376 3.625e-02 25.866 1.607e-147 [ 0.867, 1.009]
VIX Index[0:5] -0.0249 3.782e-02 -0.657 0.511 [-9.899e-02,4.926e-02]
VIX Index[0:22] 0.0493 2.102e-02 2.344 1.909e-02 [8.064e-03,9.044e-02]
Volatility Model
========================================================================
coef std err t P>|t| 95.0% Conf. Int.
------------------------------------------------------------------------
scale 0.9986 8.081e-02 12.358 4.420e-35 [ 0.840, 1.157]
========================================================================
Covariance estimator: robust
Zig-Zag estimation¶
A small repetitions of the previous two steps can be used to implement a so-called zig-zag estimation strategy.
[8]:
for i in range(5):
print(i)
vol_mod = ZeroMean(res.resid.dropna(), volatility=GARCH(p=1, o=1, q=1))
vol_res = vol_mod.fit(disp="off")
variance[22:] = vol_res.conditional_volatility**2.0
fv = FixedVariance(variance, unit_scale=True)
mod = HARX(vix, lags=[1, 5, 22], volatility=fv)
res = mod.fit(disp="off")
print(res.summary())
0
1
2
3
4
HAR - Fixed Variance (Unit Scale) Model Results
=======================================================================================
Dep. Variable: VIX Index R-squared: 0.876
Mean Model: HAR Adj. R-squared: 0.876
Vol Model: Fixed Variance (Unit Scale) Log-Likelihood: -1935.74
Distribution: Normal AIC: 3879.48
Method: Maximum Likelihood BIC: 3899.96
No. Observations: 1237
Date: Tue, Nov 05 2024 Df Residuals: 1233
Time: 17:50:48 Df Model: 4
Mean Model
=================================================================================
coef std err t P>|t| 95.0% Conf. Int.
---------------------------------------------------------------------------------
Const 0.5602 0.152 3.681 2.323e-04 [ 0.262, 0.858]
VIX Index[0:1] 0.9381 3.616e-02 25.940 2.388e-148 [ 0.867, 1.009]
VIX Index[0:5] -0.0262 3.774e-02 -0.693 0.488 [ -0.100,4.781e-02]
VIX Index[0:22] 0.0499 2.099e-02 2.380 1.733e-02 [8.810e-03,9.109e-02]
=================================================================================
Covariance estimator: robust
Direct Estimation¶
This model can be directly estimated. The results are provided for comparison to the previous FixedVariance estimates of the mean parameters.
[9]:
mod = HARX(vix, lags=[1, 5, 22], volatility=GARCH(1, 1, 1))
res = mod.fit(disp="off")
print(res.summary())
HAR - GJR-GARCH Model Results
==============================================================================
Dep. Variable: VIX Index R-squared: 0.876
Mean Model: HAR Adj. R-squared: 0.875
Vol Model: GJR-GARCH Log-Likelihood: -1932.61
Distribution: Normal AIC: 3881.23
Method: Maximum Likelihood BIC: 3922.19
No. Observations: 1237
Date: Tue, Nov 05 2024 Df Residuals: 1233
Time: 17:50:48 Df Model: 4
Mean Model
================================================================================
coef std err t P>|t| 95.0% Conf. Int.
--------------------------------------------------------------------------------
Const 0.7796 1.190 0.655 0.513 [ -1.554, 3.113]
VIX Index[0:1] 0.9180 0.291 3.156 1.597e-03 [ 0.348, 1.488]
VIX Index[0:5] -0.0393 0.296 -0.133 0.894 [ -0.620, 0.541]
VIX Index[0:22] 0.0632 6.353e-02 0.994 0.320 [-6.136e-02, 0.188]
Volatility Model
========================================================================
coef std err t P>|t| 95.0% Conf. Int.
------------------------------------------------------------------------
omega 0.2357 0.250 0.944 0.345 [ -0.254, 0.725]
alpha[1] 0.7091 1.069 0.664 0.507 [ -1.386, 2.804]
gamma[1] -0.7091 0.519 -1.367 0.172 [ -1.726, 0.308]
beta[1] 0.5579 0.855 0.653 0.514 [ -1.117, 2.233]
========================================================================
Covariance estimator: robust